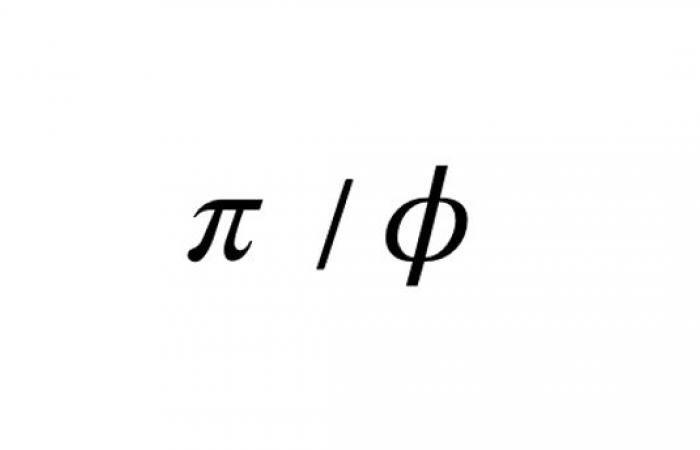The link between (pi) (pi) and (phi) (the golden ratio) has fascinated mathematicians and science enthusiasts for centuries. Although these two mathematical constants seem to belong to distinct worlds – (pi) being associated with circles and geometry, while the golden ratio is deeply linked to harmonious proportions in nature and art –, there are subtle but powerful connections between them. This article aims to demystify these links by exploring the formulas and properties that unite them, thus allowing you to add a string to your bow for your next homework, tests, or even your competitions!
Definitions and properties
Definitions of (pi)
There are multiple definitions of (pi):
- Geometric definition: (pi) = (displaystyle frac{text{the circumference of the circle}}{text{the diameter of the circle}})
- Analytical definition: (displaystyle pi = 4 sum_{n=0}^{infty} frac{(-1)^n}{2n+1})
- Trigonometric definition: (displaystyle pi = 2 int_{-1}^{1} frac{1}{sqrt{1 – x^2}} , dx)
Its approximate value is 3.14159 in decimal writing.
Definitions of (phi)
Similarly, there are multiple definitions of the golden ratio (phi):
- Algebraic definition: (displaystyle phi = frac{1 + sqrt{5}}{2}) (golden number linked to the Fibonacci sequence)
- Geometric definition: (displaystyle phi = frac{a}{b}) where (displaystyle frac{a + b}{a} = frac{a}{b}), with (a) and (b) two lengths
- Definition by continued fraction: (displaystyle phi = 1 + frac{1}{1 + frac{1}{1 + frac{1}{1 + cdots}}})
- Trigonometric definition: (displaystyle phi = 2 cosleft(frac{pi}{5}right))
Historical and philosophical origins
Historical origins of (pi)
The history of (pi) dates back to ancient times. The Egyptians and Babylonians approximated (pi) with values close to 3.16 and 3.125. In ancient Greece, Archimedes (~287-212 BC) used the method of inscribed and circumscribed polygons to approximate (pi) with remarkable precision, placing it between 3.1408 and 3.1428. Later work by Ptolemy, Liu Hui (China), and other mathematicians continued to refine this constant.
Historical origins of (phi)
The golden ratio, denoted (phi), finds its roots in ancient Greece with the work of Euclid, who studied it in his work The Elements as a solution of a geometric proportion. It appears in the construction of the regular pentagon and in classical architecture, such as the Parthenon. The concept was reinterpreted during the Renaissance by artists, such as Leonardo da Vinci, who used it for its aesthetic qualities in their works.
Appearance in nature and art
Appearance of (pi)
In nature: (pi) is related to the circular or spherical shapes found in planetary orbits, bubbles and waves. It also governs oscillatory phenomena, such as sound vibrations or the movement of pendulums, described by trigonometric functions.
In art and architecture: (pi) appears in the design of domes, such as those of the Pantheon, and in abstract art, where artists like Kandinsky use circular shapes to create rhythms based on this constant.
Appearance of (phi)
In nature: the golden ratio is omnipresent in the logarithmic spirals of shells, galaxies and in phyllotaxis (leaf arrangement), where plants often follow patterns based on (phi) to optimize their growth.
In art and architecture: Used since ancient times, the golden ratio is incorporated into works such as the Parthenon and Renaissance paintings. Artists like Leonardo da Vinci and Salvador Dalí applied it to create harmonious compositions, seen as ideal.
Mathematical relationships
Link in geometry and regular polygons
A major link between (pi) and (phi) appears in the geometry of regular polygons, notably the pentagon. In a regular pentagon, the ratio of the diagonals to the sides is given by (phi). Moreover, (pi) occurs in the internal angles of the pentagon. For example, we can connect (phi) to (pi) by the following trigonometric expression: (displaystyle phi = 2 cosleft(frac{pi}{5}right)).
This equation shows how (phi) is related to (pi) through the cosine of an angle associated with the regular pentagon. Shapes like the dodecahedron also obey proportions related to (phi), with geometric relationships involving (pi).
Link in continued fractions
(phi) and (pi) are also connected by continued fractions. A famous continued fraction for (pi)discovered by Ramanujan, highlights complex links between these two constants: (displaystyle frac{4}{pi} = 1 + frac{1}{3 + frac{4}{5 + frac {9}{7 + frac{16}{9 + cdots}}}}).
well that (phi) does not appear directly here, continued fractions are also used to express (phi)revealing interesting parallels in their irrational representations.
Link in infinite series and Fibonacci numbers
(phi) is closely related to the Fibonacci sequence, where each term is the sum of the previous two. The ratio between two successive terms of this sequence converges to (phi). On the other hand, infinite series involving (pi) share similar structures. For example, Wallis' infinite product series for (pi) contains recurring patterns similar to Fibonacci growth patterns: (displaystyle pi = 2 cdot prod_{n=1}^{infty} frac{4n^2}{4n^2 – 1}) .
This convergence of infinite series for (pi) and the properties of (phi) in the Fibonacci sequence illustrate a conceptual connection in how these constants describe infinite structures.
Link in logarithmic curves and spirals
Logarithmic spirals, found in nature (e.g. shells or galaxies), show a subtle connection between (pi) and (phi). These spirals follow a growth law linked to (phi)while being described using trigonometric functions involving (pi).
The general shape of a logarithmic spiral is given by: (displaystyle r = e^{btheta}), where (displaystyle theta) is measured in radians (i.e. in multiples of (displaystyle pi)). This interconnection between (pi) and (phi) through geometric curves shows their relationship in natural growth phenomena and their use in geometry.
Use in physics and cosmology
Role in physics and cosmology of (pi)
Wave mechanics: (pi) is present in solutions of wave equations, such as the Schrödinger equation, describing the wave behavior of particles.
Electromagnetism: Coulomb's law, which describes the force between charges, uses (pi) in the calculation of electric fields.
Thermodynamics: (pi) appears in equations related to thermal cycles, showing the link between geometry and physical properties.
Geometry of the universe: (pi) is fundamental in calculations on the curvature of space-time in cosmological models, such as those of Friedmann-Lemaître-Robertson-Walker.
Role in physics and cosmology of (phi)
Growth Models: Used in exponential and logarithmic growth models, (phi) describes natural processes such as phyllotaxis.
Natural phenomena: Manifested in the shape of spiral galaxies and other natural structures, illustrating the importance of golden proportions.
Cosmological constants: (phi) appears in certain theories exploring the expansion of the universe and the formation of galactic structures.
Mathematical anecdotes and curiosities
The digits of (pi) in popular culture
Literary references: the famous author Jules Verne mentions (pi) in his novel Twenty thousand leagues under the sea. In this book, Captain Nemo mentions that “the ratio between the circumference and the diameter of a circle is a constant”thus emphasizing the importance of (pi) even in fiction.
Music and (pi) : the composer Béla Bartók incorporated (pi) in his music. In his work microcosmsome melodies are built on numerical sequences based on the numbers of (pi)creating a unique relationship between mathematics and music.
Curiosities related to (phi)
The Fibonacci sequence: a lesser known fact is that the relationships between successive terms of the Fibonacci sequence converge to (phi). In fact, the more terms we take in the following, the closer this relationship gets to (displaystyle phi). For example, (displaystyle frac{F_5}{F_4} = frac{5}{3} approx 1.666) and (displaystyle frac{F_6}{F_5} = frac{8}{5 } = 1.6). We observe that these ratios tend towards (displaystyle phi approx 1.618) as (n) increases.
Modern architecture: many contemporary architects are inspired by (phi) to design buildings. The famous architect Le Corbusier used proportions based on (phi) to create harmonious spaces. Its design method, modulesis based on human dimensions integrated into a structure proportional to the golden ratio.
Trivia about memorizing (pi)
Memorization competitions: memorization competitions (pi) have existed for decades, where participants attempt to recite as many decimal places as possible. The current record is 70,000 decimal places, set by the Chinese Suresh Kumar in 2005. This phenomenon has even given rise to memory schools that teach specific techniques for memorizing (pi).
Poems of (pi) : poems called piems are written so that the number of letters in each word corresponds to a digit of (pi). For example, the first word could contain three letters, the second one letter, the third four letters, etc. It's a creative way to celebrate this mathematical constant.
Modern apps
Applications of (pi)
Computer science and cryptography: (pi) is used in pseudo-random number generation algorithms, which is essential for securing communications in cryptography.
Data visualization: in pie charts, (pi) is crucial for determining the proportions and angles of the segments.
Numerical simulation: Monte Carlo methods, which solve complex problems by random sampling, often estimate (pi) and facilitate integration calculations.
Applications of (phi)
Design and architecture: (phi) is used to create aesthetic structures. Modern architects integrate its proportions to achieve visual harmony.
Biological modeling: (phi) models the arrangement of leaves on stems (phyllotaxis) and optimizes plant growth in agriculture.
Graphics and interfaces: in graphic design, (phi) is applied to create attractive layouts, improving user experience.
Conclusion
The links between (pi) and (phi) reveal a fascinating interconnection between mathematics, art and nature. Their presence in areas such as the Fibonacci sequence, geometric properties and practical applications demonstrates that these constants are not just abstractions, but essential elements of our understanding of the world. Although outside the curriculum, these concepts provide a very good mathematical culture on the subject, which can always be useful for competitive exams or later!
You can find the mega-directory which contains all the competition records and the answers. You can also access all our other math resources!