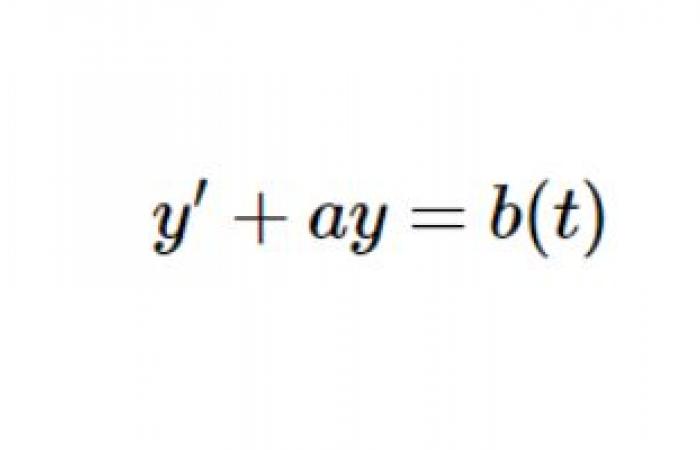Absent from ECE/ECS programs, differential equations are making a comeback in the applied mathematics curriculum. This concept must therefore be mastered at your fingertips.
But what is a differential equation?
A differential equation is an equation that relates a function to its derivatives. This function is the unknown, which is generally denoted ( y ), and depends on a variable, frequently denoted ( t ) or ( x ).
It describes how one quantity changes depending on another, such as the speed of an object which depends on time. These equations are used to model various phenomena, such as population growth, the movement of objects or temperature changes.
There are different types of differential equations and, thus, different methods for solving them.
First order differential equations
First order differential equations are equations of the form [ y’ + ay = b
where ( b ) is a continuous function on an interval ( I ) and ( t in I ).
L’homogeneous equation associated with ( (E) ) is ( y’ + ay = 0 (E_{0}) ).
The solutions of ( (E_{0}) ) are all functions ( g
The solutions of ( (E)) are the sum of the solutions of ( (E_{0}) ) and a particular solution of ( (E)) .
If (b) is a constant, so is the particular solution.
If ( b ) is not a constant, the subject guides the student in his research.
Second order differential equations
Second order differential equations are equations of the form ( y” + ay’ + by = c
where ( c) is a continuous function on an interval ( I ) and ( t in I ).
L’homogeneous equation associated with ( (E) ) is ( y” + ay’ + by = 0 (E_{0}) ).
L’characteristic equation of ( (E) ) is (r^{2} + ar + b = 0 (E_{c}) ).
If ( (E_{c}) ) admits a unique solution on ( I ) denoted ( r_{0} ), then the solutions of ( (E) ) on ( I ) are all the functions of the form:
[ g
If ( (E_{c}) ) admits two solutions on ( I ) denoted ( r_{1} ) and ( r_{2} ), then the solutions of ( (E) ) on (I ) are all functions of the form:
[ g
The solutions of ( (E)) are the sum of the solutions of ( (E_{0}) ) and a particular solution of ( (E)) .
If ( c ) is a constant, so is the particular solution.
If ( c ) is not a constant, the subject guides the student in his research.
The trajectory
The trajectory of a differential equation ( (E)) on( I ) is of the set ({ (t, y
We can obtain a unique trajectory by imposing initial conditions of the type ( y(t_{0}) = y_{0})
If it is a first order differential equation, an initial condition will be required to obtain a unique trajectory.
If it is a second order differential equation, two initial conditions will be required to obtain a single trajectory.
We call equilibrium trajectory any trajectory associated with a constant solution.
A trajectory converges if ( y
Solve a linear differential system with constant coefficients
Soit ( I in mathbb{R} ).
We call a homogeneous linear differential system with constant coefficients a system of the form:
[
(S) begin{cases}
x’_1
where ( t in I) and (x_1, dots, x_n ) are n functions of the variable (t), differentiable on (I), and (a_{11}, dots , a_{nn} ) are (n^2) real.
The goal of solving this system is to find the functions (x_1, dots, x_n).
Step 1
Let’s rewrite the system in matrix form:
On pose pour tout (t in I) :
[
X
Then, the system ((S)) can be written as (X’
Attention : the following steps are only possible if A is diagonalizable!
Step 2
We diagonalize (A) in order to write it in the form:
(A = PDP^{-1}), where (D = begin{pmatrix} lambda_1 & 0 \ 0 & ddots & 0 \ 0 & 0 & lambda_n end{pmatrix} )
(D) is a diagonal matrix that contains the eigenvalues of (A) on its diagonal.
(P) is an invertible matrix composed of the eigenvectors associated with the eigenvalues of (A), organized in columns (be careful to take the same order as for D!)
Step 3
On pose (Y
We obtain, by derivation,[begin{align}
Y’
On a alors : (Y’
), car (D=P^{-1}AP )
Let (Y
)
(
Y’
)
(
Y’
)
(
Y’
)
(forall i in I, y_i
On a therefore (Y
Step 4
We find (X
Step 5 (if requested)
We solve the system with respect to imposed initial conditions.
Simply place the (t) in our system ( X
: considering the system ( (S) X’
Example
Troubleshoot the system:[
begin{cases}
x’
Step 1
Let’s move on to matrix writing. We obtain:[
X’
Step 2
Diagonalisons A.
Do not hesitate to consult this article if you are not comfortable with the methods of diagonalizing a matrix.
Let (lambda in mathbb{R}),
(
lambda text{ is an eigenvalue of A} Leftrightarrow A-lambda I = 0
)
(
A-lambda I = begin{pmatrix}
-lambda & 1 & 1 \
-1 & 2 – lambda & 1 \
1 & 0 & 1 – lambda end{pmatrix}
)
We use the Gauss pivot method
We do (L_{1}leftrightarrow L_{3}):[
begin{pmatrix}
1 & 0 & 1-lambda \
-1 & 2-lambda & 1 \
-lambda & 1 & 1
end{pmatrix}
]
Then (L_{2}leftarrow L_{2}+L_{1}) and (L_{3}leftarrow L_{3}+lambda L_{1}) :[
begin{pmatrix}
1 & 0 & 1-lambda \
0 & 2-lambda & 2 -lambda \
0 & 1 & -lambda^{2} + lambda + 1
end{pmatrix}
]
We perform a case disjunction
For (2 – lambda ne 0), we do (L_{2}leftarrow frac{1}{(2 -lambda)L_{2}}):[
begin{pmatrix}
1 & 0 & 1-lambda \
0 & 1 & 1 \
0 & 1 & -lambda^{2} + lambda + 1
end{pmatrix}
]
Which simplifies the calculations of (L_{3}leftarrow L_{3}- L_{2}):[
begin{pmatrix}
1 & 0 & 1-lambda \
0 & 1 & 1 \
0 & 0 & -lambda^{2} + lambda
end{pmatrix}
]
On pose ( A_{lambda} = begin{pmatrix}
1 & 0 & 1-lambda \
0 & 1 & 1 \
0 & 0 & -lambda^{2} + lambda
end{pmatrix})
begin{align}
lambda text{ is an eigenvalue of A} & Leftrightarrow -lambda^{2} + lambda = 0 \
& Leftrightarrow lambda (1 – lambda) = 0 \
& Leftrightarrowlambda = 0 text{or}lambda =
end{align}
For (2 – lambda = 0), let (lambda = 2)
So (A – lambda I = A – 2I)[ A – 2I = begin{pmatrix}
1 & 0 & -2 \
0 & 0 & 0 \
0 & 1 & -1
end{pmatrix}
]
We observe that the second column is zero, thus the rank of the matrix is less than or equal to 2, therefore 2 is an eigenvalue of A.
Thus, the eigenvalues of A are ( fbox {(0, 1 text {and} 2)} ).
We then calculate the eigenspaces associated with 0, 1 and 2
Let ( X = begin{pmatrix} x \ y \ zend{pmatrix}),
For eigenvalue 0:
(
begin{align}
X in E_{0} & Leftrightarrow (A-0I)X = O \
& Leftrightarrow begin{cases} x + z = 0 \ y + z = 0 end{cases} \
& Leftrightarrow begin{cases} x = – z \ y = – z end{cases} \
& Leftrightarrow X in text{Vect}begin{pmatrix} 1 \ 1 \ – 1 end{pmatrix}
end{align}
)
Ainsi ( fbox {( E_{0} = text{Vect}begin{pmatrix} 1 \ 1 \ -1 end{pmatrix} )} )
For eigenvalue 1:
(
A_{1} = begin{pmatrix}
1 & 0 & 0\
0 & 1 & 1 \
0 & 0 & 0
end{pmatrix}
)
(
begin{align}
X in E_{1} & Leftrightarrow A_{1}X = O \
& Leftrightarrow begin{cases} x = 0 \ y + z = 0 end{cases} \
& Leftrightarrow begin{cases} x = 0 frac{1}{2} x \ y = – z end{cases} \
& Leftrightarrow X in text{Vect}begin{pmatrix} 0 \ 1 \ – 1 end{pmatrix}
end{align}
)
Ainsi ( fbox {( E_{1} = text{Vect}begin{pmatrix} 0 \ 1 \ -1 end{pmatrix} )} )
For eigenvalue 2:
(
A – 2I = begin{pmatrix}
-2 & 1 & 1 \
-1 & 0 & 1 \
1 & 0 & -1
end{pmatrix}
)
(
begin{align}
X in E_{2} & Leftrightarrow (A-2I)X = O \
& Leftrightarrow begin{cases} -2x + y + z = 0 \ -x + z = 0 \ x – z = 0 end{cases} \
& Leftrightarrow begin{cases} 2x + y + x = 0 \ x = z end{cases} \
& Leftrightarrow begin{cases} -x + y = 0 \ x = z end{cases} \
& Leftrightarrow begin{cases} y = x \ x = z end{cases} \
& Leftrightarrow X in text{Vect}begin{pmatrix} 1 \ 1 \ 1 end{pmatrix}
end{align}
)
Ainsi ( fbox {(E_{2} = text{Vect}begin{pmatrix} 1 \ 1 \ 1 end{pmatrix} )} )
A is of order 3 and has three eigenvalues, so ( fbox {( text{A is diagonalizable } )} ).
We can then write (A) in the form (A=PDP^{-1})
with (
D = begin{pmatrix}
0 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & 2
end{pmatrix}
)
And ( P = begin{pmatrix}
1 & 0 & 1 \
1 & 1 & 1 \
-1 & -1 & 1
end{pmatrix})
Let’s calculate ( P^{-1}) using the Gaussian pivot method. If you don’t know how to invert a matrix, you can consult this article.[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
1 & 1 & 1 & 0 & 1 & 0 \
-1 & -1 & 1 & 0 & 0 & 1
end{array} right]
On a :
]
We do: ( L_{2} leftarrow L_{2}+L_{1}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
0 & 1 & 0 & -1 & 1 & 0 \
-1 & -1 & 1 & 0 & 0 & 1
end{array} right]
]
Then ( L_{3} leftarrow L_{3}+L_{1}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
0 & 1 & 0 & -1 & 1 & 0 \
0 & -1 & 2 & 1 & 0 & 1
end{array} right]
]
And ( L_{3} leftarrow L_{3}+L_{2}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
0 & 1 & 0 & -1 & 1 & 0 \
0 & 0 & 2 & 0 & 1 & 1
end{array} right]
]
Then ( L_{3} leftarrow frac{1}{2}L_{3}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
0 & 1 & 0 & -1 & 1 & 0 \
0 & 0 & 1 & 0 & frac{1}{2} & frac{1}{2}
end{array} right]
]
And ( L_{1} leftarrow L_{1}-L_{3}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 0 & 1 & -frac{1}{2} & -frac{1}{2} \
0 & 1 & 0 & -1 & 1 & 0 \
0 & 0 & 1 & 0 & frac{1}{2} & frac{1}{2}
end{array} right]
]
Ainsi ( fbox {( P^{-1} = begin{pmatrix}
1 & -frac{1}{2} & -frac{1}{2} \
-1 & 1 & 0 \
0 & frac{1}{2} & frac{1}{2}
end{pmatrix} ) } )
Step 3
Let (Y
We obtain, by derivation,
On a alors : (Y’
), car (D=P^{-1}AP )
Let (Y
X’
Y’
end{cases}
)
Soit ( (C_{1}, C_{2}, C_{3}) in mathbb{R}^{3} )
(
Y’
end{cases}
)
On a donc (Y
C_{3}e^{2t}
end{pmatrix})
Step 4
Let us find (X
X
end{pmatrix}[ fbox {( begin{cases}
C_{1} + C_{3}e^{2t}\
C_{1} + C_{2}e^{t} + C_{3}e^{2t} \
– C_{1} – C_{2}e^{t} + C_{3}e^{2t}
end{cases} )}
]
)
So the solution of the initial system is
Do not hesitate to do this exercise again and again until you have understood and memorized the different steps of solving a system of differential equations.
You can then explore this concept in more depth thanks to these articles:
You can also deepen your mastery by challenging yourself with these articles:
You can find here the mega-directory which contains all the competition records and the answers. You can also access all our other math resources here!
- -