The couch problem, a nearly 60-year-old mathematical puzzle, was likely solved by a South Korean student as part of his thesis at the University of Michigan in the United States. It has been readable in pre-publication since December 2 on the ArXiv website.
Everyone has experienced the hassle of moving a sofa down a hallway — a situation immortalized in the series Friends during a scene past posterity. Well, it is quite possible that this crucial difficulty for humanity (at least for anyone who is embarking on a move) is no longer one.
Jineon Baek, a postdoctoral researcher at Yonsei University in Seoul, did his thesis on this mathematical problem at the University of Michigan, putting forward a proposed solution. On December 2, his thesis was put online as pre-publication (therefore not yet reviewed by mathematician peers) on the ArXiv site.
A particular sofa, that of Gerver
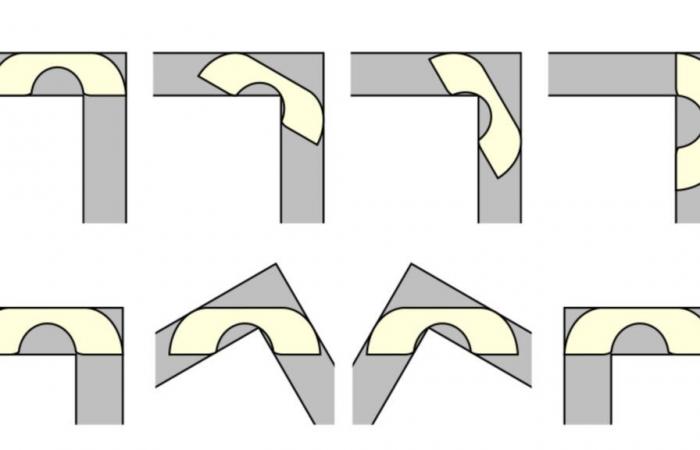
The sofa problem, also called the sofa problem, dates from 1966 and is easily understood, including by non-mathematicians. Leo Moser, an Austrian-Canadian mathematician, is trying to find the largest surface area of a sofa that can be moved horizontally in a hallway one unit wide and has a right angle.
But if the problem simply arises, its resolution is difficult. This is a more complicated calculation than it seems, because you have to succeed in matching the correct surface of the furniture with the movement that the sofa must make in space, taking into account the constraints (the right angle and each part of the corridor).
Previously, with different studies, it was established that the maximum area was in the interval between 2.2195 units and 2.37 units.
The lower limit of this interval (therefore 2.2195) was demonstrated in 1992 by the mathematician Joseph Gerver, professor at Rutgers University, in New Jersey (United States). The teacher had also determined a particular shape for this sofa: a cube composed of a semi-circular hollow and rounded edges.
The upper bound (2.37) was found via a computer-assisted method in 2018 by Dan Romik and Yoav Kallus, two mathematicians working at the University of California at Davis and the University of Santa Fe, New Mexico, respectively.
The final solution to the sofa problem
Jineon Baek, to solve the problem, started again with the shape of the sofa developed by Joseph Gerver. After a hundred pages of demonstration, he finally arrived at the following answer: in a corridor one unit wide, the maximum possible surface area of the sofa is indeed the one that Gerver had found initially, that is to say 2 ,2195 units.
Its solution must still be verified by different mathematicians, but it could well be that, 58 years after its formulation, this is the end of this mathematical problem.